LeetCode 53.最大子数组和 题解

题目描述

题目链接

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

样例

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：
                                                                                                                                                                                                                                                                                                      
输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

---

算法1

(动态规划) $O(n)$

由于本题需要求数组中最大子数组的和，那么如果暴力枚举区间的起点、终点的话，需要 $O(n^2)$ 的时间复杂度

同时，我们能够看出，数组中每个位置代表的不仅仅是一种情况，而是一类状态的情况总和，因此可以考虑使用动态规划的思想

思路：

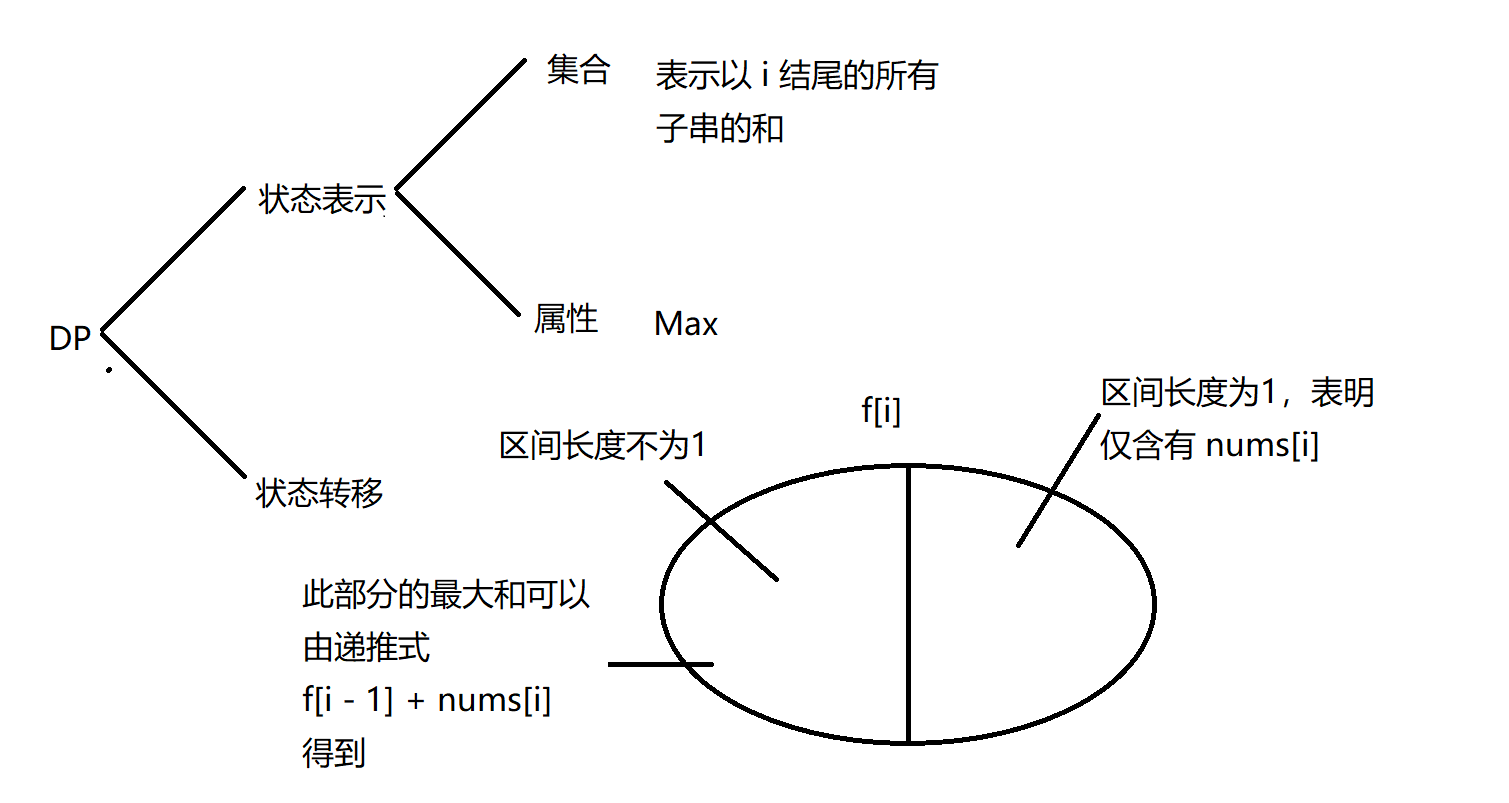
• 可以定义 $f(n)$数组来表示以 i 结尾的位置最大子数组的和
• 根据定义，我们可以分析得到:
  • 若区间长度为 1， 那么 f[i] = nums[i];
  • 若区间长度大于 1， 那么 f[i] = f[i - 1] + nums[i]

因此，可以得到动态规划的转移方程为：
$ f[i] = max(f[i - 1] + nums[i], nums[i])$

同时，我们可以发现：

不必开辟 $O(n)$ 的额外空间，只需要两个变量动态更新 $f[i]$ 与 $f[i - 1]$ 即可

C++ 代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        int pre = 0, ans = nums[0];

        for(int i = 0; i < n; i ++)
        {
            pre = max(pre + nums[i], nums[i]);
            ans = max(pre, ans);
        }

        return ans;
    }
};